HW 2: Percolation

An exercise in using Disjoined Sets. Unfortunately, this is the only homework self-studying students are able to take - though I suspect that's because the other 3 are non-coding.

Prerequisites to running the code.

Instructions: https://fa22.datastructur.es/materials/hw/hw2/

Solution: https://github.com/tomthestrom/cs61b/tree/master/hw2/hw2

As per the instructions, I implemented 2 classes in this assignment:

• Percolation

  • to model the percolation using

• PercolationStats

  • to estimate the percolation treshold, using Monte Carlo simulation

Introduction

Percolation. Given a composite systems comprised of randomly distributed insulating and metallic materials: what fraction of the materials need to be metallic so that the composite system is an electrical conductor? Given a porous landscape with water on the surface (or oil below), under what conditions will the water be able to drain through to the bottom (or the oil to gush through to the surface)? Scientists have defined an abstract process known as percolation to model such situations.

The model. We model a percolation system using an N-by-N grid of sites. Each site is either open or blocked. A full site is an open site that can be connected to an open site in the top row via a chain of neighboring (left, right, up, down) open sites. We say the system percolates if there is a full site in the bottom row. In other words, a system percolates if we fill all open sites connected to the top row and that process fills some open site on the bottom row. (For the insulating/metallic materials example, the open sites correspond to metallic materials, so that a system that percolates has a metallic path from top to bottom, with full sites conducting. For the porous substance example, the open sites correspond to empty space through which water might flow, so that a system that percolates lets water fill open sites, flowing from top to bottom.)

In the diagrams below, you can see that in the system on the left, the water is able to start in a site on the top row and trickle down through empty sites until it reaches an empty site on the bottom row.

Whereas on the right, the water in the site on the top row has no way of trickling down to an open site on the bottom row.

Source: UC Berkeley CS61B Fa22 - homework 2 (https://fa22.datastructur.es/materials/hw/hw2/images/percolates.png)

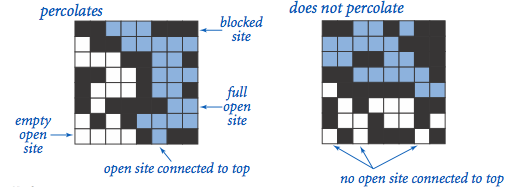
Percolation

Requirements

To model a percolation system, in the hw2 package, complete the Percolation data type with the following API:

public class Percolation {
   public Percolation(int N)                // create N-by-N grid, with all sites initially blocked
   public void open(int row, int col)       // open the site (row, col) if it is not open already
   public boolean isOpen(int row, int col)  // is the site (row, col) open?
   public boolean isFull(int row, int col)  // is the site (row, col) full?
   public int numberOfOpenSites()           // number of open sites
   public boolean percolates()              // does the system percolate?
}

Corner cases. By convention, the row and column indices are integers between 0 and N − 1, where (0, 0) is the upper-left site: Throw a java.lang.IndexOutOfBoundsException if any argument to open(), isOpen(), or isFull() is outside its prescribed range. The constructor should throw a java.lang.IllegalArgumentException if N ≤ 0.

Performance requirements. Your code must use the WeightedQuickUnionUF class! Do not reimplement the Union Find ADT. The constructor should take time proportional to N^2, all methods should take constant time plus a constant number of calls to the union-find methods union(), find(), connected(), and count().

Your numberOfOpenSites() method must take constant time. Part of the goal of this assignment is to learn how to cast one problem (Percolation) in terms of an already solved problem (Disjoint Sets, a.k.a Union Find).

The problem with percolation. In a famous scientific problem, researchers are interested in the following question: if sites are independently set to be open with probability p (and therefore blocked with probability 1 − p), what is the probability that the system percolates? When p equals 0 (no site is open), the system does not percolate; when p equals 1 (all sites are open), the system percolates. The plots below show the site vacancy probability p versus the percolation probability for 20-by-20 random grid (top) and 100-by-100 random grid (bottom).

Source: https://fa22.datastructur.es/materials/hw/hw2/images/percolation-threshold20.png

Source: https://fa22.datastructur.es/materials/hw/hw2/images/percolation-threshold100.png

When is sufficiently large, there is a threshold value such that when a random N-by-N grid almost never percolates, and when , a random N-by-N grid almost always percolates. No mathematical solution for determining the percolation threshold has yet been derived. Your task is to write a computer program to estimate.

Implementation

About

This was basically about solving a connectedness problem. The system percolates in case the top and bottom are connected, thus we can also say that they are in the same set. The fastest datastructure to check for connectedness is a Weighted Quick Union (with path compression).

At the beginning, all sites (x, y positions on the grid) are closed and all of them are in their own set (disjoined sets). To keep track of each site, I have a private instance attribute representing my (disjoined sets) of type WeightedQuickUnionUF called grid.

As the sites are gradually, randomly, opening - in case two open sites are next to each other, I union them.

To know whether a system percolates, I need to find out, whether a site at the top and a site at the bottom are connected.

To help with this, I created 2 virtual "sentinel" sites, one at the top, the other one at the bottom, so to check whether a system percolates, I just need to check whether they're within the same set.

To meet the performance requirements on isOpen(int row, int col) - to return in constant time, I have another instance attribute called valGrid, which is a boolean array that mirrors the grid. Sites that are open are assigned the value true. I decided to use a one-dimensional array for this, though the API to the end-user of the Percolation class asks for row, col attributes, I later convert it into 1 dimension - this way I have the exact mirror in both the disjoined set grid and the valGrid. To ensure both arrays are mirrored, grid's size is larger by 2 to accomodate for the virtual sites that are stored at the last 2 indexes.

Code

package hw2;

import edu.princeton.cs.algs4.WeightedQuickUnionUF;

/**
 * Percolation data type
 * Models a percolation system
 */
public class Percolation {

    /**
     * Used to define the size of the grid -> N x N
     */
    private int N;
    /**
     * 1-dimensional, holds N by N grid
     * Row nr as index / N
     * Col nr as index % N
     */
    private WeightedQuickUnionUF grid;

    /**
     * Mirrors grid
     * Sets value at x, y to true, if site is opened
     */
    private boolean[] valGrid;
    /**
     * Nr of opened sites
     */
    private int openSitesNr;

    /**
     * The value of the virtual top Index
     */
    private int virtualTopIndex;

    /**
     * The value of the virtual bottom Index
     */
    private int virtualBottomIndex;

    public Percolation(int N) {
        if (N <= 0) {
            throw new IllegalArgumentException("N must be > 0");
        }

        this.N = N;
        int size = N * N;

        //grid + index for virtual top, + index for virtual bottom
        grid = new WeightedQuickUnionUF(size + 2);
        valGrid = new boolean[size];
        virtualTopIndex = size;
        virtualBottomIndex = size + 1;
        openSitesNr = 0;
    }

    /**
     * Opens site at row, col
     * If possible - connects with neighboring sites
     */
    public void open(int row, int col) {
        if (!isValidIndex(row, col)) {
            throw new IndexOutOfBoundsException();
        }
        int index = getIndexFromRowCol(row, col);

        if (isOpen(row, col)) {
            return;
        }

        valGrid[index] = true;
        openSitesNr++;
        union(row, col);
    }

    /**
     * Returns whether a site at row, col is open
     */
    public boolean isOpen(int row, int col) {
        int index = getIndexFromRowCol(row, col);

        //default (closed) value is null
        return valGrid[index];
    }

    /**
     * Indicates whether a site has been filled
     */
    public boolean isFull(int row, int col) {
        if (!isValidIndex(row, col)) {
            throw new IndexOutOfBoundsException();
        }

        int index = getIndexFromRowCol(row, col);
        return grid.connected(index, virtualTopIndex);
    }

    /**
     * Returns the number of open sites
     */
    public int numberOfOpenSites() {
        return openSitesNr;
    }

    /**
     * Returns whether the system percolates - is full/filled connecting the top to the bottom
     */
    public boolean percolates() {
        return grid.connected(virtualTopIndex, virtualBottomIndex);
    }

    /**
     * Converts x, y / row, col to one-dimensional value for grid
     */
    private int getIndexFromRowCol(int row, int col) {
       return N * row + col;
    }

    /**
     * Check if requested index in bounds
     */
    private boolean isValidIndex(int row, int col) {
        int index = getIndexFromRowCol(row, col);

        return index >= 0 && index < valGrid.length;
    }

    /**
     * Creates unions in all possible directions
     */
    private void union(int row, int col) {
        int index = getIndexFromRowCol(row, col);

        unionAbove(row, col);
        unionRight(row, col);
        unionLeft(row, col);
        unionBottom(row, col);

    }

    /**
     * If possible - connects element at  row, col with the element above itself
     */
    private void unionAbove(int row, int col) {
        int index = getIndexFromRowCol(row, col);

        // if top row, connect with virtualTop - fill the site
        if (row == 0) {
            grid.union(virtualTopIndex, index);
            return;
        }

        int indexAbove = getIndexFromRowCol(row - 1, col);

        //if site above the current site is open - union them
        if (valGrid[indexAbove]) {
            grid.union(indexAbove, index);
        }
    }

    /**
     * If possible - connects element at  row, col with the element to the right of itself
     */
    private void unionRight(int row, int col) {
        //col at the right edge;
        if (col == N - 1) {
            return;
        }

        int index = getIndexFromRowCol(row, col);
        int indexRight = getIndexFromRowCol(row, col + 1);

        if (valGrid[indexRight]) {
            grid.union(indexRight, index);
        }
    }

    /**
     * If possible - connects element at  row, col with the element to the left
     */
    private void unionLeft(int row, int col) {
        //col at the left edge;
        if (col == 0) {
            return;
        }

        int index = getIndexFromRowCol(row, col);
        int indexLeft = getIndexFromRowCol(row, col - 1);

        if (valGrid[indexLeft]) {
            grid.union(indexLeft, index);
        }
    }

    /**
     * If possible - connects element at  row, col with the element to the bottom
     */
    private void unionBottom(int row, int col) {
        int index = getIndexFromRowCol(row, col);
        int indexBottom = getIndexFromRowCol(row + 1, col);
        boolean isLastRow = row == N - 1;

        /*
        * if is in the last row and site is connected to virtualTop index (isFull),
        * connect with virtual bottom - we have a percolating system
        *  */

        if (isLastRow && isFull(row, col)) {
            grid.union(index, virtualBottomIndex);
        }

        if (!isLastRow && valGrid[indexBottom]) {
            grid.union(index, indexBottom);
        }
    }
}

PercolationStats

Requirements

Monte Carlo simulation. To estimate the percolation threshold, consider the following computational experiment:

• Initialize all sites to be blocked.

• Repeat the following until the system percolates:

  • Choose a site uniformly at random among all blocked sites.

  • Open the site.

• The fraction of sites that are opened when the system percolates provides an estimate of the percolation threshold.

To perform a series of computational experiments, in the hw2 package, complete the PercolationStats data type with the following API:

public class PercolationStats {
   public PercolationStats(int N, int T, PercolationFactory pf)   // perform T independent experiments on an N-by-N grid
   public double mean()                                           // sample mean of percolation threshold
   public double stddev()                                         // sample standard deviation of percolation threshold
   public double confidenceLow()                                  // low endpoint of 95% confidence interval
   public double confidenceHigh()                                 // high endpoint of 95% confidence interval
}

Implementation

I think the code below is fairly straightforward, this was the easy part of the homework. :)

/**
 * Perform T independent experiments on an N-by-N grid
 * Calculates:
 *  mean
 *  standard deviation
 *  low endpoint of 95% confidence interval
 *  high endpoint of 95% confidence interval
 */
public class PercolationStats {
    /**
     * Defines grid size as NxN
     */
    private int N;

    /**
     * Defined by parameter T
     */
    int experimentsAmount;

    /**
     * Sample mean of percolation threshold
     * Calculated in the constructor
     */
    private double mean;

    /**
     * Sample standard deviation of percolation threshold
     * Calculated in the constructor
     */
    private double stdDev;

    private PercolationFactory percolationFactory;

    /**
     * Calculates the data as / specification on init.
     * @param N - int grid size
     * @param T - int sample size
     * @param pf - an instance of PercolationFactory
     */
    public PercolationStats(int N, int T, PercolationFactory pf) {
        if (N <= 0 || T <= 0) {
            throw new IllegalArgumentException("N and T must be higher than 0, N: " + N + " T: " +T);
        }

        this.N = N;
        experimentsAmount = T;
        percolationFactory = pf;

        //ratio of open sites to total sites - till percolation reached for each T;
        double[] openSitesRatioLog = new double[experimentsAmount];

        for (int i = 0; i < T; i++) {
            openSitesRatioLog[i] = (double) sitesTillNPercolates() / Math.pow(N, 2);
        }

        mean = StdStats.mean(openSitesRatioLog, 0, openSitesRatioLog.length);
        stdDev = StdStats.stddev(openSitesRatioLog, 0, openSitesRatioLog.length);

    }

    /**
     * sample mean of percolation threshold
     * */
    public double mean() {
        return mean;
    }

    /**
     * sample standard deviation of percolation threshold
     * */
    public double stddev() {
        return stdDev;
    }

    /**
     * low endpoint of 95% confidence interval
     */
    public double confidenceLow() {
        return mean - ((1.96 * stdDev)/Math.sqrt(experimentsAmount));
    }

    /**
     * high endpoint of 95% confidence interval
     */
    public double confidenceHigh() {
        return mean + ((1.96 * stdDev)/Math.sqrt(experimentsAmount));
    }

    /**
     * Returns the nr of the sites opened till
     */
    private int sitesTillNPercolates() {
        Percolation p = percolationFactory.make(this.N);

        while (!p.percolates()) {
           openRandomSite(p);
        }

        return p.numberOfOpenSites();
    }

    /**
     * Get a random nr. in the range of our grid - used for generating random coords
     */
    private int getRandomSiteCoord() {
       return StdRandom.uniform(0, N);
    }

    /**
     * Opens a random site - with checks - if the randomly generated site is already opened, tries to open a new one
     */
    private void openRandomSite(Percolation p) {
       int row = getRandomSiteCoord();
       int col = getRandomSiteCoord();

       while (p.isOpen(row, col)) {
           row = getRandomSiteCoord();
           col = getRandomSiteCoord();
       }

       p.open(row, col);
    }

    public static void main(String args[]) {
        PercolationStats ps = new PercolationStats(50, 50, (new PercolationFactory()));

        System.out.println(ps.mean());
        System.out.println(ps.stddev());
        System.out.println(ps.confidenceLow());
        System.out.println(ps.confidenceHigh());
    }
}