Project 1: Deques

Prerequisites to running the code.

Instructions: https://fa22.datastructur.es/materials/proj/proj1/

Solution: https://github.com/tomthestrom/cs61b/tree/master/proj1

This is were the course got interesting for me.

Deque

• stands for "double ended queue"

• sequence container with dynamic size, that can be expanded or contracted on both ends

About the project

The main task was to implement a Deque ADT. The first implementation felt quite natural, since we were asked to use a Linked List based implementation. The second one used an array based implementation, so I had to figure out an implementation of a circular array.

In the second part, I used my implementation of the Deque API to be the underlying data structure of a Guitar Hero clone. This part only included writing a couple lines to hook up my data structures with the rest of the Guitar Hero clone code, that had been provided by the CS 61 B instructors.

The project also includes some unit tests for the Deque data structures, some of them provided by the authors, more extensive written by me.

Deque API

Specifically, any deque implementation must have exactly the following operations:

• public void addFirst(T item): Adds an item of type T to the front of the deque. You can assume that item is never null.

• public void addLast(T item): Adds an item of type T to the back of the deque. You can assume that item is never null.

• public boolean isEmpty(): Returns true if deque is empty, false otherwise.

• public int size(): Returns the number of items in the deque.

• public void printDeque(): Prints the items in the deque from first to last, separated by a space. Once all the items have been printed, print out a new line.

• public T removeFirst(): Removes and returns the item at the front of the deque. If no such item exists, returns null.

• public T removeLast(): Removes and returns the item at the back of the deque. If no such item exists, returns null .

• public T get(int index): Gets the item at the given index, where 0 is the front, 1 is the next item, and so forth. If no such item exists, returns null. Must not alter the deque!

In addition, we also want our two deques to implement these two special methods:

• public Iterator<T> iterator(): The deques objects we’ll make are iterable (i.e. Iterable<T>) so we must provide this method to return an iterator.

• public boolean equals(Object o): Returns whether or not the parameter o is equal to the deque. o is considered equal if it is a deque and if it contains the same contents (as determined by the generic T’s equals method) in the same order. (You’ll need to use the instance of keywords for this. Read here for more information)

1. Linked List Deque #

Additional requirements

Your operations are subject to the following rules:

• add and remove operations must not involve any looping or recursion. A single such operation must take “constant time”, i.e. execution time should not depend on the size of the deque. This means that you cannot use loops that go over all/most elements of the deque.

• get must use iteration, not recursion.

• size must take constant time.

• Iterating over the LinkedListDeque using a for-each loop should take time proportional to the number of items.

• Do not maintain references to items that are no longer in the deque. The amount of memory that your program uses at any given time must be proportional to the number of items. For example, if you add 10,000 items to the deque, and then remove 9,999 items, the resulting memory usage should amount to a deque with 1 item, and not 10,000. Remember that the Java garbage collector will “delete” things for us if and only if there are no pointers to that object.

Implementation

About

The underlying implementation is a Doubly Linked List, it's items are instances of a nested class - DequeNode, in order to not deal with special cases when the Deque is empty, I used a sentinel node.

I did some extras such as:

1. get(int index):

   • in case the element's index is in the second half of the Deque, iterate from the back - thus the real lookup is basically O(N/2)

2. getRecursive(int index):

   • a recursive implementation of get

   • also searches from the back, in case the index is in the 2nd half of the Deque.

Code

/**
 * Deque implementation based on specs for project1... and some tuning :)
 * @param <T>
 */
public class LinkedListDeque<T> implements Iterable<T>, Deque<T> {

    /**
     * One DequeNode - a unit used by LinkedListDeque :)
     * @param <T>
     */
    private static class DequeNode<T> {
        public T item;
        public DequeNode prev;
        public DequeNode next;

        public DequeNode(T i, DequeNode p, DequeNode n) {
            item = i;
            prev = p;
            next = n;
        }
    }

    private class LinkedListeDequeIterator implements Iterator<T> {

        /*
        * Index of the currently visited position
        */
        private int vizPos;

        /**
         * HEAD pointer
         */
        private DequeNode<T> nextNode;

        private LinkedListeDequeIterator() {
            vizPos = 0;
        }
        @Override
        public boolean hasNext() {
            return vizPos < size;
        }

        @Override
        public T next() {
            nextNode = vizPos == 0 ? sentinel.next : nextNode.next;
            vizPos += 1;

            return nextNode.item;
        }
    }


    private DequeNode<T> sentinel;
    private int size;

    public LinkedListDeque() {
        sentinel = new DequeNode<>(null, null, null);
        size = 0;
    }

    /* adds an item to the beginning */
    @Override
    public void addFirst(T item) {
        DequeNode<T> newNode = new DequeNode<>(item, sentinel, sentinel.next);

        if (size == 0) {
            sentinel.next = newNode;
            sentinel.prev = newNode;

            //in case it's the first added item, both (prev&next) pointers point to sentinel
            newNode.next = sentinel;
        } else {
            //set the previously first prev pointer to newNode
            sentinel.next.prev = newNode;
            //set sentinel's next pointer to the nexNode - new first element
            sentinel.next = newNode;
        }

        size += 1;
    }

    /* appends an item to the end */
    @Override
    public void addLast(T item) {
        DequeNode<T> newNode = new DequeNode<>(item, sentinel.prev, sentinel);

        if (isEmpty()) {
            sentinel.next = newNode;
            sentinel.prev = newNode;

            //in case it's the first added item, both (prev&next) pointers point to sentinel
            newNode.prev = sentinel;
        } else {
            //set the previously last node's next pointer to newNode
            sentinel.prev.next = newNode;
            //set sentinel's prev pointer to the nexNode - new last element
            sentinel.prev = newNode;
        }

        size += 1;
    }

    @Override
    public boolean isEmpty() {
        return size == 0;
    }

    @Override
    public int size() {
        return size;
    }

    /* removes and returns the first element of the deque */
    @Override
    public T removeFirst() {
        if (isEmpty()) {
            return null;
        }

        DequeNode<T> firstNode = sentinel.next;
        T firstItem = firstNode.item;


        if (size == 1) {
            sentinel.next = null;
            sentinel.prev = null;
        } else {
            //set the previously 2nd Node's pointer to sentinel
            sentinel.next.prev = sentinel;
            //set sentinel's next pointer to the 2nd (before removal), now new first element
            sentinel.next = firstNode.next;
        }

        size -= 1;

        return firstItem;
    }

    /* removes and returns the last element of the deque */
    @Override
    public T removeLast() {
        if (isEmpty()) {
            return null;
        }

        DequeNode<T> lastNode = sentinel.prev;
        T lastItem = lastNode.item;


        if (size == 1) {
            sentinel.next = null;
            sentinel.prev = null;
        } else {
            //sent the next pointer of the (before deletion) 2nd to last element to sentinel (now it's the new last)
            sentinel.prev.next = sentinel;
            sentinel.prev = lastNode.prev;
        }

        size -= 1;

        return lastItem;
    }

    /**
     * Get element by index using iteration (indexing from the front)
     * @param index
     * @return
     */
    @Override
    public T get(int index) {
        if (index > size - 1) {
            throw new IndexOutOfBoundsException();
        }

        boolean iterFromFront = shouldSearchFromFront(index, getBreakPointIndex());

        DequeNode<T> nextNode = iterFromFront ? getFromFront(index) : getFromBack(index);

        return nextNode.item;
    }


    /**
     * Get element by index using recursion (indexing from the front)
     * @param index
     * @return
     */
    public T getRecursive(int index) {
        if (index > size - 1) {
            throw new IndexOutOfBoundsException();
        }
        boolean shouldSearchFromFront = shouldSearchFromFront(index, getBreakPointIndex());

        DequeNode<T> nextNode = shouldSearchFromFront ?
                getRecFromFront(sentinel.next, index) :
                getRecFromBack(sentinel.prev, getReverseIndex(index));

        return nextNode.item;
    }

    @Override
    public Iterator<T> iterator() {
        return new LinkedListeDequeIterator();
    }

    /*
       Returns whether or not the parameter o is equal to the deque.
        o is considered equal if it is a deque and if it contains the same contents
     */
    @Override
    public boolean equals(Object o) {
        if (!(o instanceof LinkedListDeque) || size() != ((LinkedListDeque<?>) o).size()) {
            return false;
        }

        Iterator curObj = iterator();
        Iterator compObj = ((LinkedListDeque<?>) o).iterator();

        while(curObj.hasNext() && compObj.hasNext()) {
            if (curObj.next() != compObj.next()) {
                return false;
            }
        }

        return true;
    }

    /**
     * Prints the items in the deque from first to last, separated by a space.
     * Once all the items have been printed, prints out a new line.
     */
    @Override
    public void printDeque() {
        if (size > 0) {
            StringBuilder itemString = new StringBuilder();
            for (T itemValue : this) {
                itemString.append(itemValue).append(" ");
            }

            System.out.println(itemString);
        }

        System.out.println();
    }

    /*
        Helper method for getRecursive
         */
    private DequeNode getRecFromFront(DequeNode nextNode, int index) {
        if (index == 0) {
            return nextNode;
        }

        return getRecFromFront(nextNode.next, index - 1);
    }

    /**
     * Helper method - reversing the index - useful when looking from the back
     * @param index
     * @return
     */
    private int getReverseIndex(int index) {
        return (size - 1) - index;
    }
    /*
    Helper method for getRecursive
    Expects index provided from behind so the last (9th) element from a 9 item list is at index=0
     */
    private DequeNode getRecFromBack(DequeNode nextNode, int reverseIndex) {
        if (reverseIndex == 0) {
            return nextNode;
        }

        return getRecFromBack(nextNode.prev, reverseIndex - 1);
    }


    /**
     * Iterate from the front until index and return DequeNode at said index
     * @param index
     * @return
     */
    private DequeNode getFromFront(int index) {
        DequeNode nextNode = sentinel.next;

        int i = 0;
        while (i < index) {
            nextNode = nextNode.next;
            i += 1;
        }

        return nextNode;
    }

    /*
     * Iterate from the back until index and return DequeNode at said index
    *  */
    private DequeNode getFromBack(int index) {
        DequeNode nextNode = sentinel.prev;

        int i = size - 1;
        while (i > index) {
            nextNode = nextNode.prev;
            i -= 1;
        }

        return nextNode;
    }

    /*
    Returns size / 2 if size even
    (size + 1) / 2 if uneven

    Eg. for size 7 -> getHalfIndex() -> 4
    */
    private int getBreakPointIndex() {
        boolean isSizeEven = size % 2 == 0;
        return isSizeEven ? size / 2 : (size + 1) / 2;
    }

    /*
    * Determines whether we should start looking for an item from the front
    * True: start from the front
    * False: start from the end
    * */
    private boolean shouldSearchFromFront(int requestedIndex, int brPointIndex) {
        return requestedIndex < brPointIndex;
    }


}

2. Array Deque #

Additional requirements

For this implementation, your operations are subject to the following rules:

• add and remove must take constant time, except during resizing operations.

• get and size must take constant time.

• The starting size of your array should be 8.

• The amount of memory that your program uses at any given time must be proportional to the number of items. For example, if you add 10,000 items to the deque, and then remove 9,999 items, you shouldn’t still be using an array of length 10,000ish. For arrays of length 16 or more, your usage factor should always be at least 25%. This means that before performing a remove operation that will bring the number of elements in the array under 25% the length of the array, you should resize the size of the array down. For arrays under length 16, your usage factor can be arbitrarily low.

Implementation

About

An array based deque implemented using a circular array. In order for it to function, I needed to keep track of the first and last index.

Implementing this is a bit tricky, because it can easily happen, that the first index is actually at a larger index in the underlying array, than the last index.

For example, to get an element by its index, since the first element in the Deque is at firstIndex:

• we calculate the requested element's index in the circular array by adding it to the firstIndex

  • in case that the sum of those two is larger than the length of the underlying circularArray

    • we need to subtract the length of the array from this sum - to see this in practice, check out the get(int index) method.

In case we're adding elements into the deque and we fill the circularArray, we resize via resizeUpIfNecessary private method - when resizing, the size of the underlying array is doubled.

In case we're removing elements from the deque we might need to resize via resizeDownIfNecessary - we do this in case our usage ratio (R) is <= 0.25 - by reducing circularArray's length to half.

Code

public class ArrayDeque<T> implements Iterable<T>, Deque<T> {

    /**
     * Stores items added to the front and to the end
     */
    private T[] circularArray;

    /**
     * index of the first item
     */
    private int firstIndex;
    /**
     * index of the last item
     */
    private int lastIndex;

    /**
     * Number of elements that circularArray holds
     */
    private int size;

    /**
     * minimum size of underlying array as in specification
     */
    private int ITEMS_MIN_SIZE = 8;

    private class ArrayDequeIterator implements Iterator<T> {


        /*
         * Index of the currently visited position
         */
        private int vizPos;


        private ArrayDequeIterator() {
            vizPos = 0;
        }
        @Override
        public boolean hasNext() {
            return vizPos < size;
        }

        @Override
        public T next() {
            T nextItem = get(vizPos);
            vizPos++;

            return nextItem;
        }
    }
    public ArrayDeque() {
        circularArray = (T[]) new Object[ITEMS_MIN_SIZE];
        size = 0;
    }

    /**
     * Inserts items starting from the middle of the array to the left
     * In case the left size is filled till index 0 - inserting from the end
     * [null, null, null, 1, null, null, null, null]
     * insert direction:
     * [<----------- start\ /end<------------------]
     */
    @Override
    public void addFirst(T item) {
        resizeUpIfNecessary();

        int insertIndex = getNextFirstIndex();

        circularArray[insertIndex] = item;
        size += 1;
    }

    /**
     * Inserts items left to right
     * In case the right size is filled till the last index, start inserting from index 0
     * [null, null, null, 1, null, null, null, null]
     * insert direction:
     * [-----------> end\ /start------------------>]
     */
    @Override
    public void addLast(T item) {
        resizeUpIfNecessary();

        int insertIndex = getNextLastIndex();
        circularArray[insertIndex] = item;
        size += 1;
    }

    /**
     * Size provided to the user of ArrayDeque #Plateau's cave
     */
    @Override
    public int size() {
        return size;
    }

    /**
     * True if no items stored
     */
    @Override
    public boolean isEmpty() {
        return size() == 0;
    }

    /**
     * Prints the items in the deque from first to last, separated by a space.
     * Once all the items have been printed, prints out a new line.
     */
    @Override
    public void printDeque() {
        if (size > 0) {
            StringBuilder itemString = new StringBuilder();
            for (T itemValue : this) {
                itemString.append(itemValue).append(" ");
            }

            System.out.println(itemString);
        }

        System.out.println();
    }

    @Override
    public T removeFirst() {
        if (isEmpty()) {
            return null;
        }

        resizeDownIfNecessary();

        T firstItem = circularArray[firstIndex];

        circularArray[firstIndex] = null;
        size -= 1;
        //move firstIndex from right to left
        firstIndex = firstIndex + 1 < circularArray.length ? firstIndex + 1 : 0;

        return firstItem;
    }

    @Override
    public T removeLast() {
        if (isEmpty()) {
            return null;
        }

        resizeDownIfNecessary();

        T lastItem = circularArray[lastIndex];

        circularArray[lastIndex] = null;
        size -= 1;

        //move last index from left to right
        lastIndex = lastIndex - 1 >= 0 ?
                lastIndex - 1 :
                circularArray.length - 1;

        return lastItem;
    }

    /**
     * Gets item by index
     * Cycling from right to left
     */
    @Override
    public T get(int index) {
        if (index >= size()) {
            throw new IndexOutOfBoundsException();
        }

        int requestedIndex = firstIndex + index < circularArray.length ?
                firstIndex + index :
                firstIndex + index - circularArray.length;

        return circularArray[requestedIndex];
    }

    /*
       Returns whether or not the parameter o is equal to the deque.
        o is considered equal if it is a deque and if it contains the same contents
        //compares to ArrayDeques for now
     */
    @Override
    public boolean equals(Object o) {
        if (!(o instanceof ArrayDeque<?>) || size() != ((ArrayDeque<?>) o).size()) {
            return false;
        }

        Iterator curObj = iterator();
        Iterator compObj = ((ArrayDeque<?>) o).iterator();

        while(curObj.hasNext() && compObj.hasNext()) {
            if (curObj.next() != compObj.next()) {
                return false;
            }
        }

        return true;
    }

    @Override
    public Iterator<T> iterator() {
        return new ArrayDequeIterator();
    }

    private int getCircularArrayMiddle() {
        return circularArray.length / 2;
    }

    /**
     * Returns the next index to insert the first element at within circularArray
     */
    private int getNextFirstIndex() {
        int insertIndex;

        //if size 0, insert into the middle
        if (size() == 0) {
            insertIndex = getCircularArrayMiddle() - 1;
            //if size 0, set the lastIndex
            lastIndex = insertIndex;
        } else { //insertion from right to left
            insertIndex = firstIndex - 1 >= 0 ? firstIndex - 1 : circularArray.length - 1;
        }

        firstIndex = insertIndex;

        return insertIndex;
    }

    /**
     * Returns the next index to insert the last element at within circularArray
     */
    private int getNextLastIndex() {
        int insertIndex;

        //if size 0, insert into the middle
        if (size() == 0) {
            insertIndex = getCircularArrayMiddle();
            //if size 0, set the lastIndex
            firstIndex = insertIndex;
        } else { //insertion from left to right
            insertIndex = lastIndex + 1 < circularArray.length ? lastIndex + 1 : 0;
        }

        lastIndex = insertIndex;

        return insertIndex;
    }

    /**
     * Resizes the underlying array
     * In the newly created circularArray the first element is at index 0
     */
    private void resize(int capacity) {
        if (capacity < ITEMS_MIN_SIZE) {
            capacity = ITEMS_MIN_SIZE;
        }

        T[] a = (T[]) new Object[capacity];

        for (int i = 0; i < size(); i += 1) {
            a[i] = get(i);
        }

        firstIndex = 0;
        lastIndex = size() - 1;
        circularArray = a;
    }

    /**
     * Decrease size if usage below LENGTH_TO_USAGE_RATIO by RESIZE_FACTOR
     */
    private void resizeDownIfNecessary() {
        int LENGTH_TO_USAGE_RATIO = circularArray.length / 4;
        int RESIZE_FACTOR = 2;

        if ((size <= LENGTH_TO_USAGE_RATIO) && (size > 4)) {
            resize(circularArray.length / RESIZE_FACTOR);
        }
    }


    /**
     * Increase size by RESIZE_FACTOR
     */
    private void resizeUpIfNecessary() {
        int RESIZE_FACTOR = 2;
        if (size() == circularArray.length) {
            resize(circularArray.length * RESIZE_FACTOR);
        }
    }

}

3. MaxArrayDeque #

Additional requirements

A MaxArrayDeque has all of the methods that an ArrayDeque has, but it also has 2 additional methods and a new constructor:

• public MaxArrayDeque(Comparator<T> c): creates a MaxArrayDeque with the given Comparator.

• public T max(): returns the maximum element in the deque as governed by the previously given Comparator. If the MaxArrayDeque is empty, simply return null.

• public T max(Comparator<T> c): returns the maximum element in the deque as governed by the parameter Comparator c. If the MaxArrayDeque is empty, simply return null.

Implementation

About

Since MaxArrayDeque should have all the methods of the ArrayDeque, I simply extended ArrayDeque and implemented the required methods.

Code

/**
 * Can either tell you the max element in itself by using the Comparator<T> given to it in the constructor via max(),
 * or an arbitrary Comparator<T> that is different from the one given in the constructor via max(c).
 *
 * @param <T>
 */
public class MaxArrayDeque<T> extends ArrayDeque<T> {
    Comparator<T> comparator;

    MaxArrayDeque(Comparator<T> c) {
        comparator = c;
    }

    /*
    * Returns the maximum element in the deque as governed by the comparator;
    */
    public T max() {
        return maxHelper(comparator);
    }

    /*
     * Returns the maximum element in the deque as given by the parameter Comparator c
     */
    public T max(Comparator<T> c) {
        return maxHelper(c);
    }

    /**
     * Iterates over elements applying the compare function of the passed in Comparator
     * @param c
     */
    private T maxHelper(Comparator<T> c) {
        T maxEl = get(0);

        for (int i = 1; i < size(); i++) {
            if (c.compare(get(i), maxEl) > 0) {
                maxEl = get(i);
            }
        }

        return maxEl;
    }
}

Guitar Hero #

The code for most of the clone was provided, the only thing left to do was to edit GuitarString, a class which uses an Deque<Double> to implement the Karplus-Strong algorithm to synthesize a guitar string sound.

GuitarString

We want to finish the GuitarString file, which should use the deque package to replicate the sound of a plucked string. We’ll be using the Karplus-Strong algorithm, which is quite easy to implement with a Deque.

The Karplus-Algorithm is simply the following three steps:

1. Replace every item in a Deque with random noise (double values between -0.5 and 0.5).

2. Remove the front double in the Deque and average it with the next double in the Deque (hint: use removeFirst) and get()) multiplied by an energy decay factor of 0.996 (we’ll call this entire quantity newDouble). Then, add newDouble to the back of the Deque.

3. Play the double (newDouble) that you dequeued in step 2. Go back to step 2 (and repeat forever).

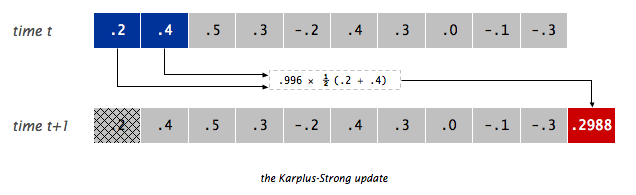
Or visually, if the Deque is as shown on the top, we’d remove the 0.2, combine it with the 0.4 to form 0.2988, add the 0.2988, and play the 0.2.

Source: UC Berkeley CS61B Fa22 - project 1 (https://fa22.datastructur.es/materials/proj/proj1/karplus-strong.png)

Implementation

About

The instructions are quite clear, so implementing this wasn't too difficult.

Code

public class GuitarString {

    ##private static final int SR = 44100;      // Sampling Rate
    private static final double DECAY = .996; // energy decay factor

    /* Buffer for storing sound data. */
     private Deque<Double> buffer;

    /* Create a guitar string of the given frequency.  */
    public GuitarString(double frequency) {
        // Create a buffer with capacity = SR / frequency. You'll need to
        // initially filled  with zeros.
        int bufferCapacity = (int) Math.round(SR / frequency);

        buffer = new LinkedListDeque<Double>();

        for (int i = 0; i < bufferCapacity; i++) {
            buffer.addFirst(0.0);
        }
    }


    /* Pluck the guitar string by replacing the buffer with white noise. */
    public void pluck() {
        // Dequeue everything in buffer, and replace with random numbers
        // between -0.5 and 0.5. You can get such a number by using:
        for (int i = 0; i < buffer.size(); i++) {
            buffer.removeFirst();
            buffer.addLast(getRandWhiteNoiseFreq());
        }
    }

    /* Advance the simulation one time step by performing one iteration of
     * the Karplus-Strong algorithm.
     * Dequeue the front sample and enqueue a new sample that is
        the average of the two multiplied by the DECAY factor.
     */
    public void tic() {
        double curFirst = buffer.removeFirst();
        double firstTwoAvg = (curFirst + buffer.get(0)) / 2;

        double nextLast = firstTwoAvg * DECAY;

        buffer.addLast(nextLast);
    }

    /* Return the double at the front of the buffer. */
    public double sample() {
        return buffer.get(0);
    }

    /**
     * Returns a nr between -0.5 and 0.5
     */
    private double getRandWhiteNoiseFreq() {
        return Math.random() - 0.5;
    }
}